[Deep한 머신러닝] Boosting 부스팅 3편 (GradientBoost Classification)

1. Boosting 부스팅 

핸즈온 머신러닝의 앙상블 (https://eumgill98.tistory.com/20)을 공부하다 보니

다른 앙상블 기법들은 이해하기 쉬웠으나 

Boosting 부스팅이 조금 더 자세히 살펴볼 필요가 있다고 생각되어서

(수식적인 이해를 할 식들이 많다) Deep한 머신러닝의첫 번째 주제로 선택하게 되었다

 

이번 글에서는 Boosting 깊이 있게 살펴 보려고 한다

포괄적인 이해를 원한다면 위의 앙상블 포스팅 링크를 참조해주기를 바란다

 

1.2.2 Gradient Boosting - Classification

지난시간 우리는 Gradient Boosting, 그중에서도 상대적으로 이해하기 쉬운 Regression에 대해서 알아 보았다

이번시간에는 Classification에 대해서 알아보도록 하겠다

 

참고한 영상 : https://www.youtube.com/watch?v=jxuNLH5dXCs 

 

이번에는 아래와 같은 데이터가 우리에게 있다

팝콘 선호 여부	나이	좋아하는 색	영화를 좋아하는지 (y값)
Yes	12	파랑	Yes
Yes	87	녹색	Yes
No	44	파랑	No
Yes	19	빨강	No
No	32	녹색	Yes
No	14	파랑	Yes

이번 데이터의 Y값은 '이진 분류'이다 

저번 Regression의 Y은 연속형 이었다면 이번에는 정확히 떨어지는 'Yes or No'이다

즉, Classification task이다

 

전체적인 과정의 흐름은 Classification과 Regression이 다르지 않다

하지만 중간중간 사용되는 함수와 손실 함수가 차이를 보이기 때문에 자세히 살펴보는 것이 중요하다

 

1. Initial prediction - Create a first leaf 

Regression에서 이부분은 Y값의 평균을 이용했다 

그렇다면 연속형이 아닌 문제에서 (평균을 구할 수 없는) 어떻게 처음 잎을 만들어 낼까?

 

바로 , log(odds)를 사용한다

 

잠깐!  여기서 Odds는 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율 이다

위와 같은 수식이 odds의 수식이다 

따라서 log(odds)는 위의 식에 log를 씌우면 된다(P(A) -> A가 일어날 확률이다)

 

즉, 우리가 가진 데이터를 예를 들어서 설명하자면 

영화를 좋아할 경우가 Yes - 4개

영화를 좋아하지 않을 경우 No - 2개 이다

 

따라서 이를 계산하면 log(odds) = log(4/2) = 0.6931 = 0.7

 

2. Calculated Pseudo-residual of probability

이제 이렇게 구한 예측값으로 Pseudo-residual을 구할 차례이다

즉, (실제값 - 예측값)을 해주면 된다

 

여기서 Yes - 0.7을 어떻게 할지 의문이 생긴다 

하지만 명심할 것!! Classification에서 특히, 이진분류인 경우 Yes = 1, No = 0으로 볼 수 있다

 

팝콘 선호 여부	나이	좋아하는 색	영화를 좋아하는지 (y값)	Residual
Yes	12	파랑	Yes	0.3
Yes	87	녹색	Yes	0.3
No	44	파랑	No	-0.7
Yes	19	빨강	No	-0.7
No	32	녹색	Yes	0.3
No	14	파랑	Yes	0.3

 

3. Trees

이제 이렇게 계산된 Residual을 통해서 Tree를 만들 차례이다

Y 값은 Residual로 Regression과 마찬가지로 잎을 3개로 제한 하였다 (물론 전에 언급한것 처럼 8~32개 까지 사용하기도 한다)

4. Transformations

Regression 처럼 각 잎의 output은 1개로 만들어 주어야한다 Regression에서는 평균을 사용했지만(물론 복잡한 수식을 변환하면 평균이란 소리) Classification에서 사용하는 방법은 조금 복잡하다

 

왜냐하면 ex) -0.7은 Probability이고 Y'(=0.7)은 log(odds)로 형태가 다르기 때문이다

즉, 우리는 Y'에 더해주기 위해서 Probability를 변환 해줄 필요가 있다

 

즉 Probability를 log(odds)로 변환해주는 것이다

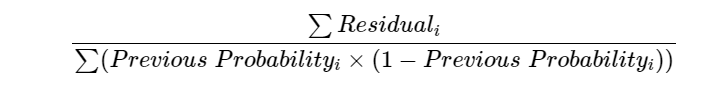
위 식을 적용해서 각 잎의 대표값을 만들어 주면 된다

 

따라서 우리가 가진 Tree로 계산하면 다음과 같다

5. Updating predictions

그럼 이제 우리는 무엇을 해야할까? 바로 예측을 새롭게 만들어주면 된다 (업데이트를 실행해주는 것이다)

뭐 어떻게 하냐고?

0.7(Y') + 학습률 a(0.8로 가정) *(해당 잎의 값 ex 1.4) = 0.7 + (0.8 * 1.4) = 1.8

 

이렇게 나온 값을 다시 가능성 Probability로 변환 해주자 (지금의 값은 log(odds) 형태이므로)

이 과정을 반복해서 Predicted Prob를 갱신해주면 아래의 결과를 구할 수 있다

팝콘 선호 여부	나이	좋아하는 색	영화를 좋아하는지 (y값)	Residual	Predicted Prob
Yes	12	파랑	Yes	0.3	0.9
Yes	87	녹색	Yes	0.3	0.5
No	44	파랑	No	-0.7	0.5
Yes	19	빨강	No	-0.7	0.1
No	32	녹색	Yes	0.3	0.9
No	14	파랑	Yes	0.3	0.9

 

6. 반복 

이제 이 과정을 반복해 주면 된다

 

7. OutPut

그럼 OutPut을 나타내는 전체 공식은 어떻게 될까?

 

간단하다 

첫 번째 데이터로 예를 들면 다음과 같다

0.7 + (0.8[학습률] * 1.4) + (0.8 * 0.6) = 2.3

엥? 2.3? 2.3은 어느 분류에 속하는 것일까?

우리가 까먹은 단계가 있다 바로 가능성 probability로 변환해주지 않은 것이다

 

이

0.9가 나왔다. 이제 이를 0or 1로 변환해주면 된다

이진 분류의 경우 threshold를 0.5로 기준잡아 분류해준다

즉, 0.9 > = 0.5 이므로 1에 해당한다

 

이런 식으로 모든 데이터를 학습하고 예측하면 결과가 나오는 것이다

 

 

 

 

---

오늘은 Gradient Boost의 Classification에 대해서 알아보았다 

다음 시간에는 Gradient Boost 계열인 Xgboost, LGBM, CatBoost에 대한 글로 돌아오겠다

위 모델들이 각종 머신러닝대회에서 좋은 결과를 휩쓸고 있으니 반드시 한번 보고 넘어가야할 모델들이다