- [추가학습 정리] 미분 공식 정리2023년 03월 12일
- Cat_Code
- 작성자
- 2023.03.12.:13

인공지능을 공부하다 보면 '미분'이라는 장치는 알지 못하면 수식 자체를 이해하지 못하는 경우가 대부분이다
특히, 문과출신인 나에게 '미분'이라는 과제는 크게 다가온다
기본적인 미분의 공식은 잘 알고 있지만
지수나, 로그 함수를 미분했을 때 만들어지는 도함수는 머리속에서 잘 그려지지 않는다
그래서 공부를 하면서 참고할려고 아래에 여러 '미분 공식'을 정리하였다
아직, 지수 및 로그 함수의 미분 결과가 왜 저렇게 나오는지 이해해보려고 노력하고 있지만
일단 수식 자체를 이해하기 위해서 아래의 공식을 활용할 것이다.
✅미분 공식 정리
1. 상수를 미분하면 0이된다
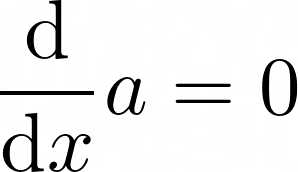
2. 상수배한 함수를 미분하는 것은 도함수에 상수배를 한 것과 같다

3. 두 함수 f(x)와 g(x)의 합과 차를 미분하는 것은 각 함수의 도함수의 합과 차와 같다 (두 함수가 모두 미분가능한 경우)
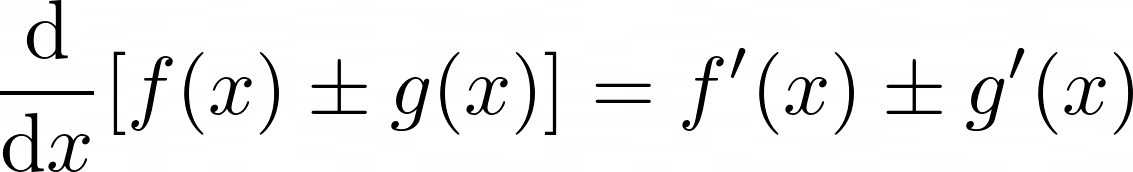
4. 두 함수 f(x)와 g(x)의 곱을 미분하는 것은 각 함수의 도함수에 다른 함수를 곱한 것의 합과 같다
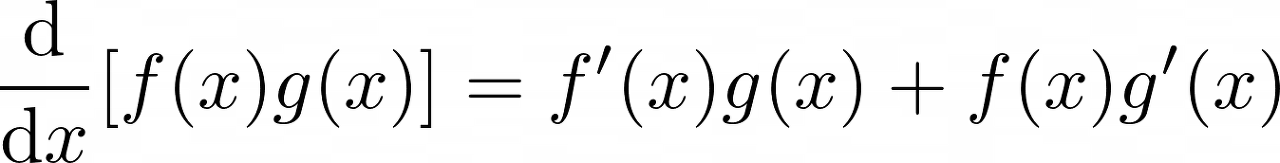
5. 두함수 f(x)와 g(x)의 나눗셈을 미분하는 것은 분자의 도함수에 분모를 곱하고, 분자에 분모의 도합수를 곱하여 뺀 값을 분모의 제곱으로 나눈 것과 같다.

6. 연쇄법칙 chain rule
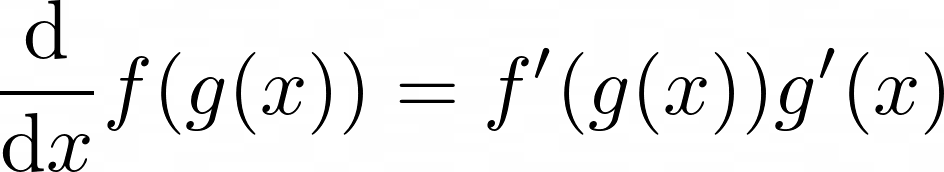
✅지수함수 및 로그함수 미분 관련 공식 정리
1. 자연 지수함수의 도함수
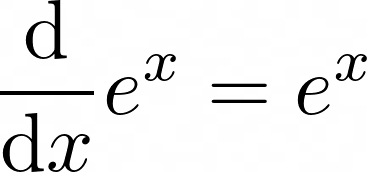
2. 지수함수의 도함수

3. 자연로그 함수의 도함수

4. 로그함수의 도함수

증명 : https://blog.naver.com/biomath2k/221871372782
[미적분] 지수함수 극한 공식 증명; 로그함수 극한 공식 증명; lnx 극한; log 극한; 지수 극한 공식
a 〉 0, a ≠ 1 일 때, 다음 등식이 성립합니다. [공식 증명] 무리수 e 의 정의를 이용합니다. 로그 극한 ...
blog.naver.com
+) 예시로 풀어보는 지수 및 로그 함수 미분
출처 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=biomath2k&logNo=221871324264

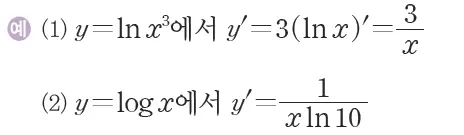
'[네이버 부스트캠프] > 🎶추가 학습 정리' 카테고리의 다른 글
[Pytorch] tensor의 연산과 인덱싱 (0) 2023.03.15 [논문리뷰 PPT] ImageNet Classification with Deep convolutional Neural Networks 논문리뷰 (0) 2023.03.10 다음글이전글이전 글이 없습니다.댓글