Entropy, CrossEntropy 그게 뭔데?

본글은 순수한 의문에 의해서 작성된 글입니다

글쓴이의 부족한 수학지식에 의해서 오류가 있을 경우가 다분하니 참고해서 읽어주시길 바랍니다

---

딥러닝 모델을 학습하다 보면 항상 마주치는 문제가있다

물론 모델이 마주치는 문제가 아니라 모델을 작성하거나 공부하는 인간이 마주치는 문제이다

 

" 바로  수식이다 "

 

수학은 많은 사람들을 혼란스럽게 만든다

 

이번 글은 그런 수식에 관한 글이다

이번 글을 시작으로 다양한 딥러닝의 수식들을 정리해보려고한다

 

물론 당장 딥러닝 모델을 학습 시키는데 완벽한 이해는 필요없는 부분이지만

우리의 슨배님들이 모두 구현 해놓았다고 

공부하지 않을 수는 없다

 

---

✅ 정보이론 : 정보량 (Quantity of information)

Entropy와 CrossEntropy를 이해하기 위해서는 우선 정보이론의 기본을 이해할 필요가 있다

정보이론은 무엇일까?

 

나의 전공이 '언론 정보'학과 이지만 내가 생각하는 정보는 우리가 이번에 다룰 정보와 많이 다르다

말장난이 마치 뼈문과 같은 느낌이지만

 

아무튼 정보이론을 살펴보자

정보이론을 간략하게 정리하자면 '정보'를 다루는 이론이다

 

여기서 정보는 우리가 생각하는 정보이다

아직 이해가 가지 않을 것이다

 

이해하기 쉽게 예시를 들어서 설명을 해보자

---

우리에게 동전 한개가 존재한다

자 그럼 이 동전을 던져서 나오는 경우의 수가 몇개 일까?

 

앞, 뒤 2개이다

 

그런데 우리는 이런 동전을 던져서 나오는 결과를 친구 '철수'에게 알려주어야 한다고 가정해보자

그리고 지금 철수와 나는 너무 멀리 떨어져 있어서 

휴대폰으로 앞면은 0, 뒷면은 1이라는 숫자로 메시지를 전달하기로 했다고 가정해보자

 

그리고 나는 동전을 5번 던져서 나오는 결과를 전송해 주었다

ex 앞, 앞, 뒤, 뒤, 앞, 뒤

약속된 표현방식으로 나타내면 - 0, 0, 1, 1, 0, 1이다

 

쉽죠?

 

이번에 조금도 난이도를 올려서 

26개의 알파벳 중 하나를 철수에게 알려준다고 했을 때 

스무고개 하듯이 예- 1, 아니오-0만을 가지고 전달한다고 가정해 보자

 

여기서 사용할 수 있는 대표적인 알고리즘은 이분 탐색이다

즉, 26개의 알파벳 중 우리가 전달하려는 알파벳의 위치에 따라서 앞쪽에 있으면 1, 뒷쪽에 있으면 0을 하면서

절반씩 줄여나가는 방식이다

 

이러한 방식을 활용하면 4~5번 만에 우리의 알파벳을 철수 에게 전달 해줄 수 있을 것이다

 

ex - 만악 우리의 알파벳이 F라면

앞 - A~M

뒤 - N~Z

1: 예 - 1

 

앞 - A ~ F

뒤 - G ~ M

2: 예 - 1

 

앞 - A ~ C

뒤 - D ~ F

3: 아니오 - 0

 

앞 - D

뒤 - E ~ F

4: 아니오 - 0

 

앞 - E

뒤 - F

5 : 아니오 - 0 -> F위치

 

즉, 이런 경우를 수식으로 표현하면 아래와 같이 다시 표현할 수 있다

 

2^질문개수 = 26

질문개수 = log_{2} 26

 

즉, 한 글자를 전달하기 위해서는 4.7개의 질문을 해야하는 것을 의미한다

하지만 이런 글자가 여러개인 경우 예를 들어서 10개의 단어를 전달한다고 한다면

10 x 4.7 = 47개의 질문을 해야한다

 

이를 일반화 하여 수식으로 나타내면

 

질문개수 =log_{2} (가능한결과의수) 이다

 

이를 처음으로 '정보' H라고 정의를 내린 사람이 R.V.L Hartley이다

그는 정보 H = log s^n이라고 정의하였다

 

즉, 이렇게 표현된 H가 정보이론에서 정보량을 의미한다

 

다시 정리하자면 정보량은 주어진 정보를 표현할때 필요한 bit의 양이라고 할 수 있습니다

 

---

✅ Entropy

그럼이제 이 정보량을 이용한 Entropy에 대해서 알아보도록 하자

앞에서 정보량을 잘 이해할 수 있었다면 크게 어렵지 않을 것이다

 

들어가기전에 정리를 하자면 정보량의 기댓값, 즉, 정보량의 평균이 Entropy이다

 

이를 수식으로 나타내면 아래와 같다

 

Entropy의 내용을 이해하기 쉽게 예시로 한번 설명해 보자

 

우리에게 면이 4개인 주사위가 있다고 가정을 해보자

그런데 이 주사위는 특별해서 1인 경우가 나올 확률이 50%이고  

나머지 2가 25%, 3,4가 각각 12.5%라고 가정해보자

 

이제 이렇게 나온 결과를 철수에게 전달한다고 했을때 - 앞의 방법을 그래도 1, 0 

이런 경우 앞의 정보량을 계산한 방법을 사용할 필요가 없다

 

왜냐하면 1인 경우가 50%로 나머지들 보다 훨씬 높기 때문이다

 

1, 2, 3,4에서 절반을 나눌 필요가 없이

 

1인 경우와 나머지로 묶으면 된다

그리고 1인경우 1, 아닌경우 0으로 해서 진행을 한다

만약 아니라면

이번에 나머지 2, 3, 4, 중에서 2는 나머지 25%의 50%차지하고 있기 때문에

2인 경우와 나머지로 묶으면 된다

 

이런식으로 확률의 분포가 다른경우에는 

이러한 방식으로 진행하면 되는데 이를 수식으로 표현하면

 

P(1) x 1 + P(2) x 2 + P(3) x 3 + P(4) x 3  *여기서 P안에 숫자는 문자열로 해당 숫자가 나올 확률로 생각해주면된다

 

= 0.5 + 0.5 + 0.375 + 0.375 

 

= 1.75 

 

즉, 주사위를 한번 던져서 나오는 숫자의 정보를 전달하기 위해서 필요한 질문의 횟수는 평균적으로 1.75번 하면되는 것이다

 

이는 각 사건이 벌어질 확률과 관계가 있다

1인 경우는 0.5

2인 경우는 0.25

3,4인 경우는 각각 0.125이다

 

이를 log_{2} ()에 대입을 하면

1인 경우 = 1

2인 경우 = 2

3,4인 경우 = 3 

으로 가능한 결과의 수는 발생할 확률의 역수인 것이다

 

하지만 이는 이산확률분포일때를 가정한다는 사실을 명심해야한다

따라서 이를 수식으로 정리하자면 위에서 본 수식인

이 나오게 되고 이를 Entropy라고 한다

 

정리하자면  entropy란 최적의 전략 하에서 그 사건을 예측하는 데에 필요한 질문 개수를 의미하. 다른 표현으로는 최적의 전략 하에서 필요한 질문개수에 대한 기댓값입니다.

 

---

✅ CrossEntropy

하지만 위의 상황에서 우리가 처음 사용했던 이분 탐색의 방법을 적용하면 어떻게 될까?

 

 1인 경우가 나올 확률이 50%이고  

나머지 2가 25%, 3,4가 각각 12.5%였다

 

이를 이분 탐색 방법을 적용하면

 

0.5 x 2 + 0.125 x 2 + 0.125 x 2 + 0.25 x 2 = 2

 

Entropy보다 0.25가 증가한 것을 확인할 수 있다

이렇게 증가한 2를 CrossEntorpy라고 할 수 있는데

 

한마디로 정리하자면 '특정 전략을 쓸 때 예상되는 질문개수에 대한 기댓값을 CrossEntropy라고 한다

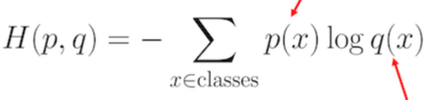
이를 수식으로 정리하면 다음과 같다

 

p= [0.5, 0.125, 0.125, 0.25]인 상황에서 

q = [0.25, 0.25, 0.25, 0.25 ]인 전략을 사용했을때 나오는 기댓값인 것이다

p가 특정 확률에 대한 참값 또는 목표 확률이고, q가 우리가 현재 학습한 확률값이라고 한다면

우리가 학습을 진행함에 따라서 q가 p에 가까워지면 CrossEntorpy가 줄어들게 될 것이다

 

---

이러한 CrossEntropy는 머신러닝과 딥러닝 학습과정에서 loss function으로 활용된다

CrossEntropy loss는 log loss로도 불리는데, 이는 CrossEntropy를 최소화 하는 것은 log likelihood를 최소화 하는 것과 같기 때문이다

 

---

✅Reference

초보를 위한 정보이론 안내서 - Cross Entropy 파헤쳐보기

 

 

 

초보를 위한 정보이론 안내서 - Entropy란 무엇일까