1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
[문제]
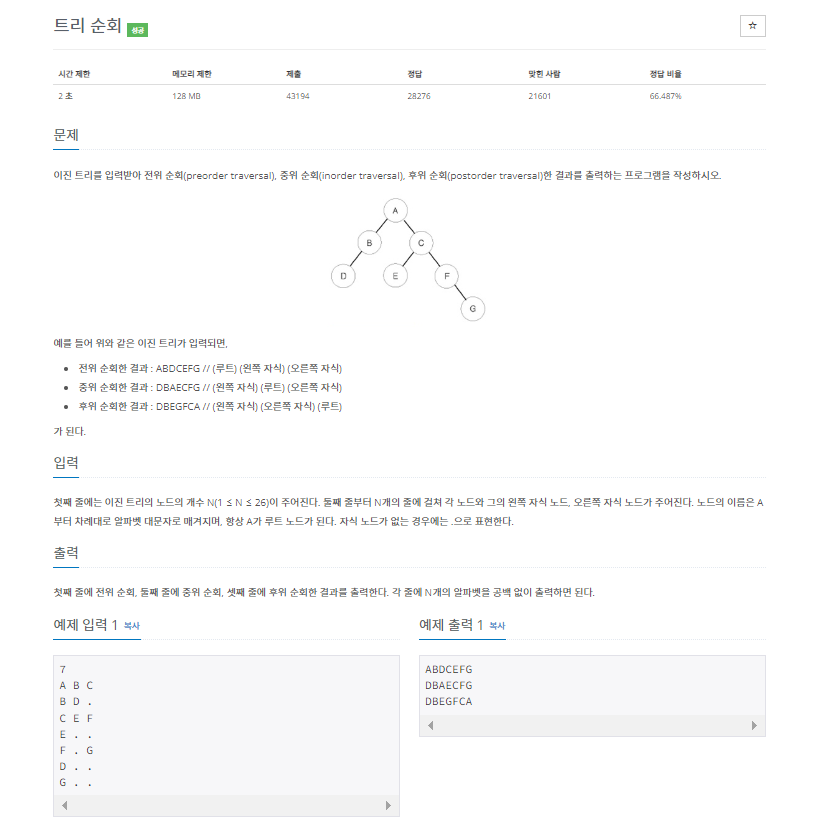
[코드]
import sys
input = sys.stdin.readline
N = int(input().strip())
#Dic 활용 해서 노드 구성
Tree = {}
for i in range(N):
node, left, right = input().strip().split()
Tree[node] = [left, right]
#input값 출력 print(Tree)
##전위 중위 후위 함수로 구현
def preorder(node): #전위
if node != '.':
print(node, end='')
preorder(Tree[node][0])
preorder(Tree[node][1])
def inorder(node): #중위
if node != '.':
inorder(Tree[node][0])
print(node, end='')
inorder(Tree[node][1])
def postorder(node): #후위
if node != '.':
postorder(Tree[node][0])
postorder(Tree[node][1])
print(node, end='')
preorder('A')
print()
inorder('A')
print()
postorder('A')참고한 코드 풀이 : link ✅
[해설]
'이진트리 탐색' 문제이다
처음 문제를 접했을 때 이진트리의 개념과 이를 탐색하는 알고리즘의 개념을 잘 몰라서 헤맸다.
그러다가 아래 블로그에서 이진트리 탐색 알고리즘에 대해서 정리한 글을 보게되었고
트리 순회(전위 순회, 중위 순회, 후위 순회)
트리를 배우면 같이 배우게 되는 개념 중 하나죠. 트리 순회에 대해 알아보겠습니다. 트리 순회에는 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder) 가 있습니다. 텍스트 추가 [그림 1]은
withhamit.tistory.com
이후에 살펴보니 재귀함수를 활용하면 쉽게 풀 수 있는 문제였다.
문제 자체가 불친절 하기때문에 전위, 중위, 후위 순회를 잘 모르는 사람이라면 풀기 어려울 것이다.
문제를 해결하기 위해서는 아래 2 가지 접근법을 정의할 필요가 있다.
- 이진 트리를 어떠한 자료 형태로 구현할 것인가?
- 전위, 중위, 후위 순회를 어떠한 방식으로 구현할 것인가?
트리 순회의 개념만 안다면 위 2가지 접근법은 쉽게 도출해낼 수 있다.
1. 이진 트리를 어떠한 자료 형태로 구현할 것인가?
답 : 물론 다양한 형태의 자료형태로 구현할 수 있다. 하지만 사전(dic)형이 가장 이상적인 접근법인것 같다
key : value 구조로 해서 구현 하면 쉽게 만들 수 있다.
ex) {'A': ['B', 'C'], 'B': ['D', '.'], 'C': ['E', 'F'], 'E': ['.', '.'], 'F': ['.', 'G'], 'D': ['.', '.'], 'G': ['.', '.']}
*여기서 '.'은 자식 노드가 없다는 것
2. 전위, 중위, 후위 순회를 어떠한 방식으로 구현할 것인가?
답 : 함수 형태로 전위, 중위, 후위 순회를 구성하여서 재귀 함수로 활용화면 쉽게 풀린다.
import sys
input = sys.stdin.readline
N = int(input().strip())
#Dic 활용 해서 노드 구성
Tree = {}
for i in range(N):
node, left, right = input().strip().split()
Tree[node] = [left, right]우선 input이 들어오는 형태가 '부모노드 자식노드 자식노드'의 형태 임으로
이를 node, left, right의 변수로 받아서 사전에 '부모노드' : [왼쪽, 오른쪽] 형태로 저장해준다
이 과정을 통해서 아래의 Tree 사전이 형성된다
{'A': ['B', 'C'], 'B': ['D', '.'], 'C': ['E', 'F'], 'E': ['.', '.'], 'F': ['.', 'G'], 'D': ['.', '.'], 'G': ['.', '.']}
그리고 이제 이 Tree 사전을 활용해서 전위, 중위, 후위 순회를 순서대로 구현해보자
전위 순회
생각보다 간단한 코드로 구현할 수 있다.
전위 순위의 개념은 다음과 같다
먼저 '부모노드'를 방문처리하고(이 문제에서는 print) 왼쪽 자식 노드로 간다 그리고 왼쪽 자식 노드에 또 다른 자식 노드가 있다면 다시 자식 노드를 방문처리하고 자식 노드의 왼쪽 자식 노드로 간다
이를 그림으로 표현하면 아래와 같다 (순회에서 오른쪽과 왼쪽 중 왼쪽이 우선순위이다)
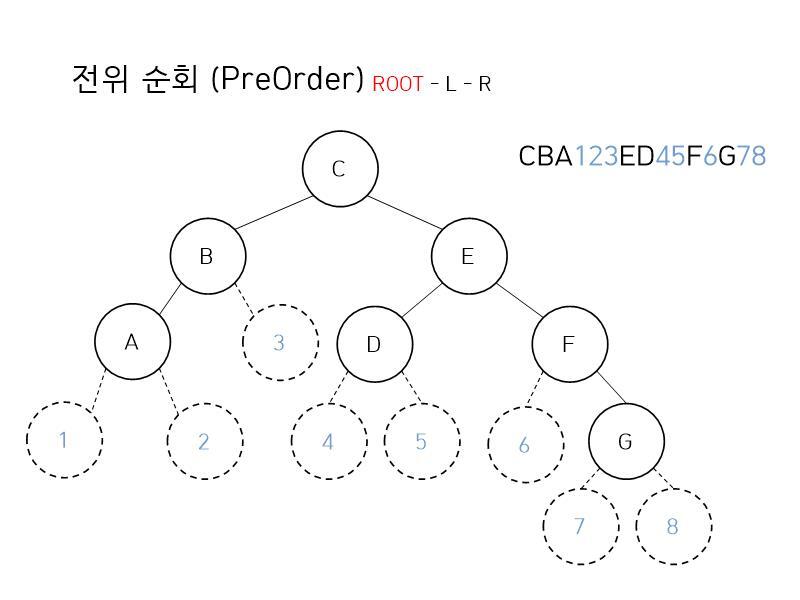
이 경우 출력의 순서는 'C - B - A - E - D - F - G'가 된다.
이를 코드로 구현하면 아래와 같다
##전위 중위 후위 함수로 구현
def preorder(node): #전위
if node != '.':
print(node, end='')
preorder(Tree[node][0])
preorder(Tree[node][1])우선 시작 node를 input으로 받는다. 그런다음 input으로 받은 노드가 '.'가 아니라면 input을 출력한다. ('.'은 값이 없는 노드이기 때문)
그런다음 왼쪽 자식 노드로 재귀함수를 적용해서 가고 - 자식 노드가 계속 존재한다면 계속 내려갈 것이다 (재귀)
그리고 각 node가 계속 출력된다. (preorder(Tree[node][0])
그런다음 왼쪽에 존재하는 모든 자식 노드가 출력 되었다면 이제 오른쪽으로 내려가면서 오른쪽 자식 노드를 출력할 것이다.(preorder(Tree[node][1])
중위 순회
중위 순회의 개념은 아래와 같다
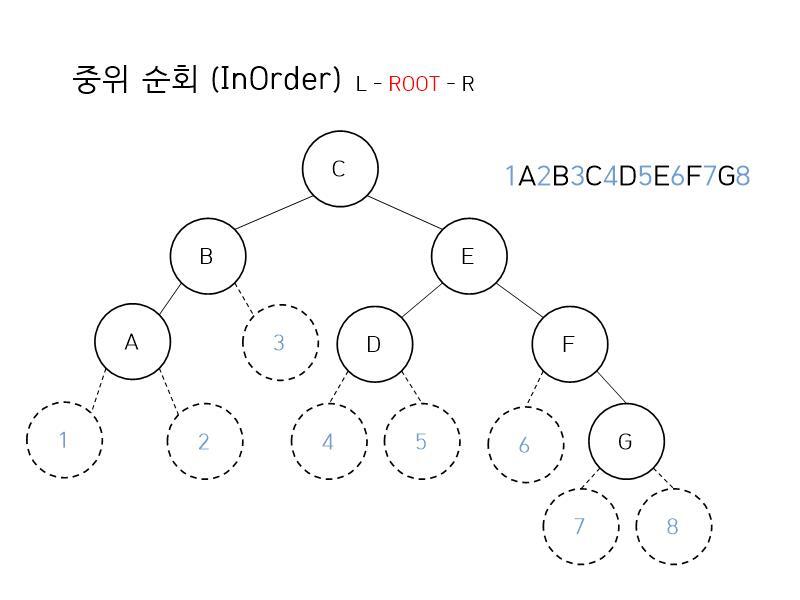
왼쪽 - 노드 - 오른쪽의 순서로 트리를 탐색한다
이를 풀어서 설명하자면 먼저 부모 노드가 주어지고 왼쪽 자식 노드가 있다면 왼쪽 자식 노드로 간다.
그리고 왼쪽 자식 노드에 또 자식 노드가 있다면 다시 그 자식 노드로 간다.
만약 없다면 현재 노드를 출력하고 다시 부모 노드로 간다. 그리고 부모 노드를 출력하고 이후에 오른쪽 자식 노드로 간다.
(쉽게 말해서 왼쪽으로 내려가면서 만약 자식 노드가 없다면 그 부모 노드를 출력하는 것이다)
이를 그림으로 표현하면 아래와 같다
이를 코드로 구현하면 아래와 같다
def inorder(node): #중위 순회
if node != '.':
inorder(Tree[node][0])
print(node, end='')
inorder(Tree[node][1])먼저 input으로 노드를 받고 만약 input이 '.'이 아니라면 즉, 값이 있다면 먼저 왼쪽 자식 노드로 내려간다 -> 그리고 또 자식 노드의 자식 노드가 있다면 계속해서 왼쪽으로 내려갈 것이다 -> 만약 왼쪽 자식이 없다면 재귀 함수는 끝나고 그다음인 print문이 실행 되서 현재 노드를 출력할 것이다
이후 다시 부모 노드로 돌아와서 이번에는 오른쪽 자식 노드를 탐색하고 위와 같은 원리로 출력될 것이다
후위 순회
후위 순회의 개념은 다음과 같다
왼쪽 - 오른쪽 - node 순서로 출력한다
이를 풀어서 설명하자면
먼저 부모 노드가 자식 노드를 갖고 있다면 (왼쪽, 오른쪽 모두) 왼쪽 자식 노드로 먼저 내려가고 값이 없을 때 까지 간다.
여기서 중위 순회와 다른 점은 오른쪽 자식 노드가 부모 노드보다 우선 순위에 있다는 것이다
즉, 중위 순회에서는 오른쪽 자식 노드는 부모 노드 출력이후에 출력 되었다면
여기에서는 왼쪽 - 오른쪽 - 부모의 순서로 출력된다.
이를 그림으로 표현하면 아래와 같다

이를 코드로 구현하면 아래와 같다
def postorder(node): #후위 순회
if node != '.':
postorder(Tree[node][0])
postorder(Tree[node][1])
print(node, end='')먼저 input으로 node가 주어지고 만약 이 노드가 값이 있다면 자식 노드 왼쪽으로 먼저 내려간다
이후 값이 없을 때 까지 내려가고 만약 값이 없다면 재귀가 끝나고
해당 자식 노드의 한단계 위의 부모 노드로 돌아가서 이번에는 오른쪽 자식 노드를 탐색한다
그리고 이후 값이 없다면 다시 한단계 위 부모 노드로 가서 부모 노드를 출력하고
이를 순서대로 진행한다
그리고 위 세가지를 시작점 'A'로 각자 실행 하면 아래와 같다
preorder('A')
print()
inorder('A')
print()
postorder('A')
>>> ABDCEFG
>>> DBAECFG
>>> DBEGFCA
'연습의 흔적들🚩 > 백준⚾' 카테고리의 다른 글
| [백준] 1240번 노드사이의 거리 파이썬 풀이 (1) | 2023.03.15 |
|---|---|
| [백준]9934번 완전 이진 트리 파이썬(Python) 풀이 (1) | 2023.03.14 |
| [백준] 1717번 집합의 표현 Python 파이썬 풀이 (0) | 2023.01.16 |
| [백준] 1339번 단어수학 Python 파이썬 풀이 (0) | 2023.01.15 |
| [백준] 1038번 감소하는 수 파이썬(Python) 풀이 (0) | 2022.12.22 |