통계와 머신러닝에서 가장 근본적이면서 중요한 분석 방법은
상관관계를 분석하는 것이다
상관관계를 살펴보기 위해서는 상관계수를 구하는 방법이 있다
상관계수는 -1 부터 +1까지의 범위로 표현할 수 있는데
+1은 완벽한 양의 상관관계를 나타내며, -1은 완벽한 음의 상관관계를 나타낸다.
0의 경우 선형관계가 없음을 의미한다.

1. 피어슨 상관계수
상관계수를 구하는 방법에는 피어슨 상관계수가 있다.
우선 상관계수는 -1~+1에 존재해야하기 때문에 정규화가 필요하다
피어슨 상관계수에서 정규화는 2가지 방법이 적용된다
| 각 변수의 평균 중심화 |
A 벡터와 B 벡터의 상관계수를 구하려고하는데 A와 B의 단위가 다르다면 -1과 +1사이로 표현할 수 없을 것이다
이를 위해서 우리는 평균 중심화를 이용한다
말로 설명하면 직관적인 이해가 되지 않지만
쉽게 말해서 각 벡터의 평균을 빼주어서 정규화 하는 방식이다.
즉, A벡터집합에 속하는 원소들을 A벡터의 평균으로 빼주는 방식이다
| 벡터 노름 곱으로 내적을 나누기 |
이 분할 정규화는 측정 단위를 제거하고 상관계수 최대 크기를 |1|로 조정한다
이를 조금더 통계용어로 표현하면 다음과 같은 단계로 구성된다

피어슨 상관계수를 수식으로 나타내면 다음과 같다

이때 변수를 벡터로 바꾸어 생각해보면 수식은 아래와 같이 변경할 수 있다
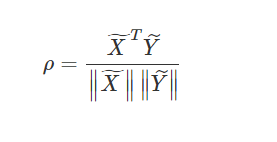
이때

은 평균 중심화된 X를 의미한다
2. 코사인 유사도
선형관계만이 두 변수간의 유사성을 판단하는 유일한 방법은 아니다
다른 방법으로 코사인 유사도가 존재한다
코사인 유사도에 대한 공식은 단순히 내적의 기하하적 공식으로 코사인 항을 구한 것이다

이때 식을 위 피어슨 상관계수와 비교해보면 매우 유사한것을 확인할 수 있다
다른점은 평균중심화가 빠졌다는 것이다
즉, 코사인 유사도에는 첫번째 정규화가 적용되어 있지 않다
따라서 같은 벡터가 입력으로 주어지고 피어슨 상관계수와 코사인 유사도를 구했을때
값이 달라질 수 있다 (물론 같을 수 있다 -> 단위가 같다면)
예를 들어서 [0, 1, 2, 3]과 [100,101,102, 103]의 피어슨 상관계수는 1이다
즉, 한 쪽 변수가 변하는 대로 다른 변수도 똑같이 변하기 때문이다
하지만 코사인 유사도는 0.808로 나온다
동일한 숫자 척도가 아니어서 완벽한 상관관계는 아니다
이를 비교하기 위한 더 간단한 예시가 있다
[-50 ~ 50]까지 offset을 만들고 [0,1,2,3]으로 구성된 vector를 만들어보자
그리고 loop를 돌면서 순차적으로 offset 하나를 vector에 더해줘서 또 다른 vector 2를 구성해주자
ex) 첫번째의 경우 -50 + [0,1,2,3] = [-50, -49, -48, -47] = v2가 된다
또한 loop과정 마다 만들어진 vector2와 원래 vector의 피어슨 상관계수와 코사인 유사도를 구해서 비교해보자
미리 보여주기 전에 피어슨 상관계수는 항상 1이 나온다 둘 벡터모두 원소가 증가하기 때문이다
하지만 코사인 유사도는 다르게 나타난다.
왜냐하면 두 벡터 사이의 척도가 다르기 때문이다
이를 그래프로 시각화 하면 아래와 같다

참고로 numpy로 직접 구현한 피어슨 상관계수와 코사인 유사도 코드는 아래와 같다
#피어슨 상관계수
def corrcoef(v1, v2):
v1m = v1 - np.mean(v1)
v2m = v2 - np.mean(v2)
return np.dot(v1m, v2m) / (np.linalg.norm(v1m) * np.linalg.norm(v2m))
#코사인 유사도
def cosin_sim(v1, v2):
return np.dot(v1, v2)/(np.linalg.norm(v1)*np.linalg.norm(v2))'ML 🐼 > 수학 ☑️' 카테고리의 다른 글
| [선형대수] 기저 (0) | 2023.05.25 |
|---|---|
| Entropy, CrossEntropy 그게 뭔데? (0) | 2023.03.27 |
| 베이즈 정리(Bayes' theorem) (0) | 2023.01.03 |